Selasa, 29 November 2011

Pembuktian Keliru 1=2 dengan kalkulus

Soal: Buktikan1=2

Jawab: Perhatikan

$1^2=1$

$2^2=2+2$

$3^2=3+3+3$

$4^2=4+4+4+4$

$\vdots$

begitu seterusnya, diperoleh

$x^{2}=\underbrace{x+x+x+\ldots+x}_{x}$

Selanjutnya turunkan kedua sisi persamaan diatas

$\frac{d}{dx}\left(x^{2}\right)=\frac{d}{dx}\left(x+x+x+\ldots+x\right)$

$2x=1+1+\ldots+1$ (sebanyak $x$ kali)

$2x=x$

$2=1$

Apa yang salah?

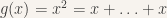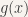Dari penjabaran diatas, kita memperoleh fungsi $g(x)=x^2$ dengan $g(x)=x^{2}=x+\ldots+x$ (sebanyak $x$ kali). Dengan mudah kita ketahui bahwa Domain (Daerah Awal) dan Image (Daerah hasil)dari $g(x)$ adalah himpunan bilangan bulat positif $\mathbb{Z}^{+}$ , dengan kata lain:

$g:\mathbb{Z}^{+}\rightarrow\mathbb{Z}^{+}$ .

Nah pertanyaanya

Apakah fungsi 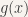$g(x)$ terturun?

Tidak, kenapa? Berdasarkan definsi turunan diperoleh

$\lim_{h\rightarrow0}\frac{g\left(x+h\right)-g\left(x\right)}{h}$

Limit diatas tidak terdefinsi, karena $g(x+h)$ tidak terdefinsi, sebab $x+h\notin\mathbb{Z}^{+}$ .
Itulah sebabnya kita mendapatkan hasil aneh bin ajaib ketika menurunkan $g(x)$

0 komentar:

Posting Komentar